Applications of Mathematics in Computer Science (MACS)
Fourier transform
Concepts:
- complex numbers;
- spatial/temporal domain;
- frequency domain;
- integer fourier transform.
Problem: frequency filtering
Applications:
- Time-series search and comparison: Shazam
- Information compression: Skype, Zoom, etc.
- Image processing
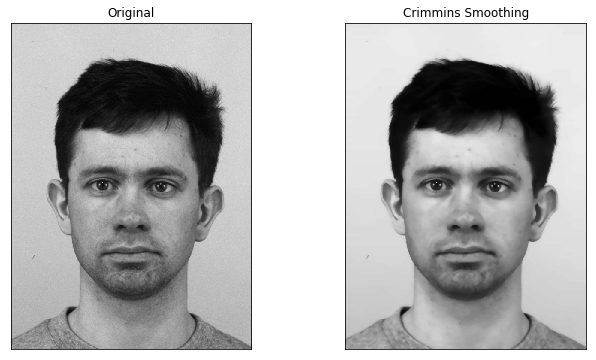
Frequency filtering
| Sound | Image |
|---|---|
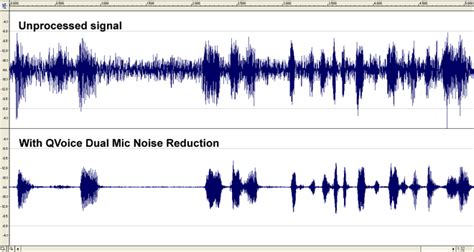 |
 |
frequency filtering
Types of filters:
- Low-pass filter
- High-pass filter
- Band-pass filter
Low-pass filter
High-pass filter

Method: Fourier transform
spacial domain $y = f(x)$ to frequency domain $y' = f(frequency)$
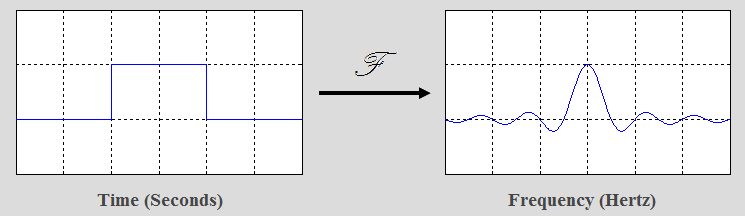
Background: complex numbers
$$x^2 + 1 = 0,\quad x = ?$$$$i = \sqrt{-1}$$
$$x = a + i\cdot b$$
$$\mathcal{R}(x)=a,\,\mathcal{I}(x)=b$$
Complex numbers: operations
$$(a + ib) + (c + id) = (a+c) + i(b+d)$$
$$(a + ib)*(c + id) = (ac - bd) + i(ad + bc)$$
$$1/(a + ib) = \frac {a} {a^2 + b^2} - \frac {b} {a^2 + b^2} i$$
...
Complex numbers: polar form
$$x = a +ib = re^{i\varphi}$$ $$r = \sqrt{a^2+b^2}$$ $$\phi = \arctan\left(\frac b a\right)$$Euler's formula
$$e^{a + ib} = e^a\cdot (\cos b + i \sin b)$$Background: sinusoidal functions
$$ y = a \sin \left(\frac {2\pi} b (x - c) \right) + d$$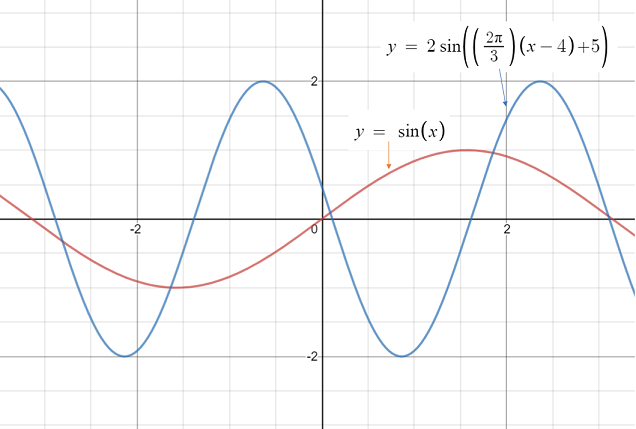
are approximation basis for smooth functions
Sinusoidal functions
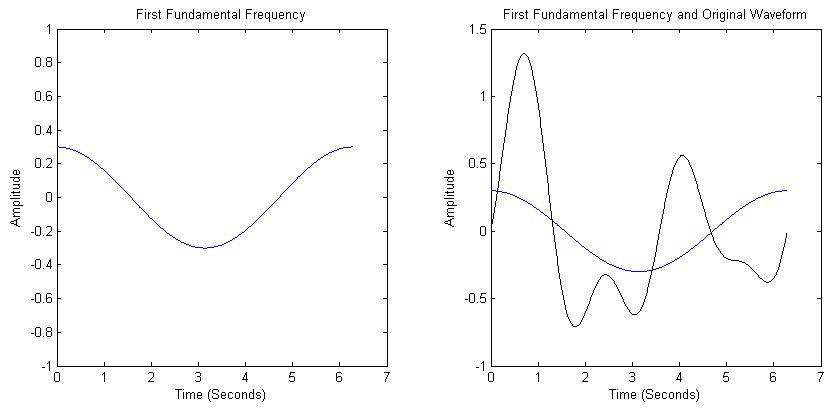
Sinusoidal functions
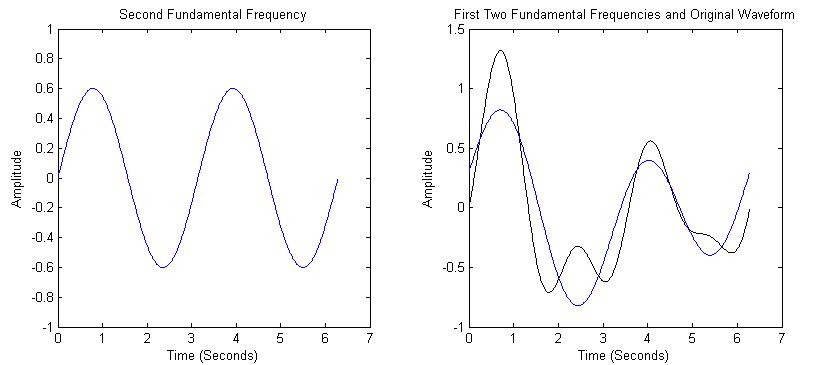
Sinusoidal functions
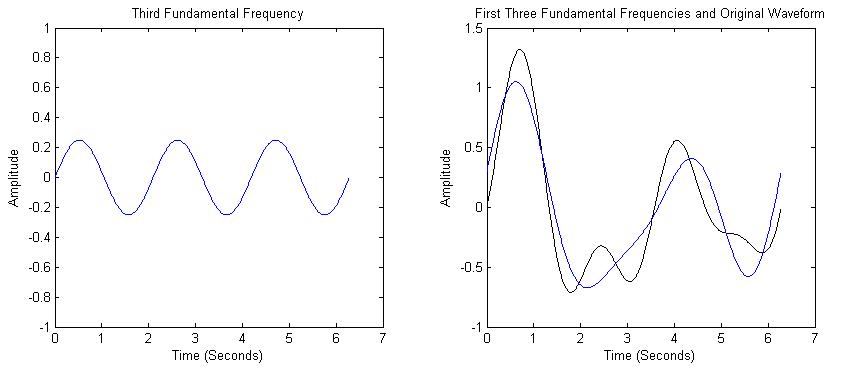
Fourier transform
$$f(t) = \sum_{n=-\infty}^{\infty}c_ne^{\frac {2\pi n} T it}$$ $$c_n = \frac 1 T \int_0^T f(t) e ^{-\frac {2\pi n} T it}dt$$Fourier transform of the saw function
$$f(t) = A\frac t T, \; 0 \le t < T$$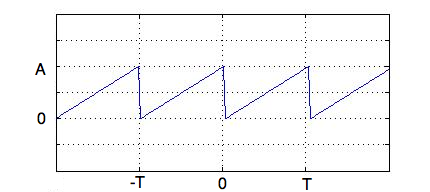
Fourier transform of the saw function
Coefficients:
$$c_0 = \frac A 2$$ $$c_n = \frac {A} {2\pi n} i$$Two terms:
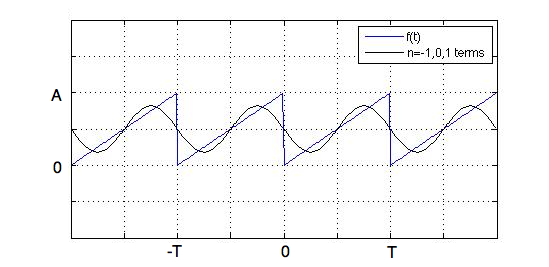
Four terms:
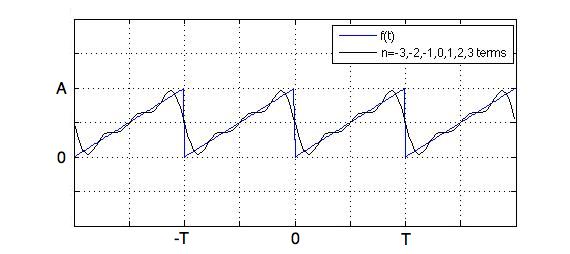
Twenty terms:
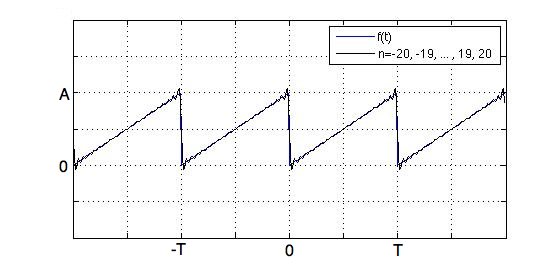
Discrete Fourier Transform
When the data is discrete (pixels, measurements):
$$X_k = \sum_{n=0}^{N-1}x_n\cdot e ^{-\frac {i2pi} N kn}$$Fast Fourier Transform (FFT) computes in $O(N \log N)$ instead of $O(N^2)$